นั้นๆเช่น เลขฐานสอง ฐานแปด และฐานสิบ ประกอบด้วยข้อมูลตัวเลขจำนวนสองหลัก (0-1) แปดหลัก (0-7) และสิบหลัก (0-9) ตามลำดับ ดังรูปในตารางที่ 1
ในระบบคอมพิวเตอร์มีการใช้ระบบเลขฐาน 4 แบบ ประกอบด้วย
1).เลขฐานสอง (Binary Number)
2).เลขฐานแปด (Octal Number)
3).เลขฐานสิบ (Decimal Number)
4).เลขฐานสิบหก (Hexadecimal Number)
ตารางที่ 1 แสดงจำนวนตัวเลข ของเลขฐานต่างๆ

1).เลขฐานสอง
คือตัวเลขที่มีค่าไม่ซ้ำกันสองหลัก ( 0 และ 1) เป็นเลขฐานเดียวที่เข้ากันได้กับ Hardware ของเครื่องคอมพิวเตอร์ได้โดยตรง เพราะการใช้เลขฐานอื่น จะสร้างความยุ่งยากให้กับเครื่องคอมพิวเตอร์อย่างมาก เช่น เลขฐานสิบมีตัวเลขที่เป็นสถานะที่ต่างกันถึง 10 ตัว ในขณะที่ระบบไฟฟ้ามีเพียง 2 สถานะ ซึ่งในช่วงเวลาหนึ่งๆมีเพียงสถานะเดียวเท่านั้น แต่ละหลักของเลขฐานสอง เรียกว่า Binary Digit (BIT)
2).เลขฐานแปด
เลขฐานแปด มีความสัมพันธ์กับเลขฐานสอง คือ เลขฐานสองจำนวน 3 หลัก แทนด้วยเลข
ฐานแปด 1 หลัก ดังนั้นเราจึงสามารถเขียนเลขฐานสอง 6 บิท แทนด้วยเลขฐานแปด 2 บิท การใช้เลขฐานแปดแทนเลขฐานสองทำให้จำนวนบิทสั้นลง
3).เลขฐานสิบ
คือตัวเลขที่มีค่าไม่ซ้ำกันสิบหลัก (0,1,2,…,9) เป็นเลขฐานที่มนุษย์คุ้นเคยและใช้ในชีวิตประจำวันมากที่สุด ตัวเลขที่มีจำนวนมากกว่า 9 ให้ใช้ 10 ซึ่งเป็นการกลับไปใช้เลข 1 และ 0 อีก เพียงแต่ค่าของ 1 เปลี่ยนไปเป็น 10 เท่าของตัวมันเอง เช่น 333 (สามร้อยสามสิบสาม) แม้จะใช้ตัวเลข 3 ทั้งหมด แต่ตำแหน่งของตัวเลขย่อมมีความหมายตามตำแหน่งของแต่ละหลักนั้น กล่าวคือ หลักหน่วยน้อยกว่าหลักสิบ 10 เท่า หลักสิบน้อยกว่าหลักร้อย 10 เท่า ตามลำดับ
4).เลขฐานสิบหก
เลขฐานสิบหก มีความสัมพันธ์กับเลขฐานสอง คือ เลขฐานสองจำนวน 4 หลัก แทนด้วย
เลขฐานสิบหก 1 หลัก ดังนั้นเราจึงสามารถเขียนเลขฐานสอง 8 บิทแทนด้วยเลขฐานสิบหก 2 บิท การใช้เลขฐานสิบหกแทนเลขฐานสองทำให้จำนวนบิทสั้นลง
การเปลี่ยนฐานเลข (Base Number Conversion)
เนื่องจากตัวเลขในแต่ละฐานมี ค่าคงที่เฉพาะ ในแต่ละหลักของตัวเอง เช่นตัวเลข 100 มีค่าเท่ากับหนึ่งร้อยในระบบเลขฐานสิบ แต่ตัวเลข 100 ในระบบ
เลขฐานสอง (อ่านว่า หนึ่ง-ศูนย์-หนึ่ง) ซึ่งมีค่าเท่ากับ 4 เป็นต้น ดังนั้น จึงไม่สามารถนำค่าของเลขฐานใดๆ ไปคำนวณเปรียบเทียบ กับเลขฐานอื่นได้โดยตรง
เมื่อต้องการคำนวณหรือเปรียบเทียบตัวเลข (ประมวลผล) จำเป็นต้องเปลี่ยนฐานเลขเหล่านั้นให้เป็นฐานเดียวกันก่อน การเปลี่ยนฐานเลขสามารถกระทำได้
หลายวิธี ในหน่วยเรียนนี้จะใช้วิธีที่สะดวกที่สุดวิธีหนึ่ง ดังนี้
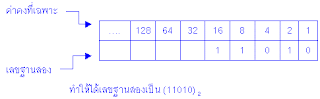
ก่อนเปลี่ยนฐานเลขใดๆ จำเป็นต้องทราบค่าคง ที่เฉพาะในแต่ละหลักของเลขฐานสองดังนี้
ตาราง แสดงค่าคงที่เฉพาะในแต่ละหลักของเลขฐานสอง
จากตาราง พบว่าค่าคงที่เฉพาะ จะมีค่าเป็น 2 เท่า จากขวาไปซ้าย
การเปลี่ยนเลขฐานสอง เป็นเลขฐานสิบ
ให้นำค่าคงที่เฉพาะที่ตรงกับเลข 1 ของฐานสองมารวมกัน เช่นจำนวน (11010)2ประกอบด้วยเลข “1” จำนวน 3 ตัว
เมื่อนำค่าคงที่เฉพาะที่ตรงกับเลข 1 มารวมกัน ทำให้ได้จำนวนในฐานสิบเป็น 16+8+2 = 26 ดังนี้


นอกจากนี้การเปลี่ยนเลขฐานสองให้เป็นเลขฐานสิบยังสามารถทำได้โดย นำตัวเลขในแต่ละตำแหน่งคูณด้วยค่าประจำตำแหน่งแล้วนำมารวมกัน
ค่าประจำตำแหน่งของเลขฐานสองเริ่มตั้งแต่ 20,21,22,…
ตัวอย่างเช่น
(1011)2 = (1x23)+(0x22)+(1x21)+(1x20)
= (1x8)+(0x4)+(1x2)+(1x1)
= 8+0+2+1
= 11
การเปลี่ยนเลขฐานสิบ เป็นเลขฐานสอง
ให้พิจารณานำค่าคงที่เฉพาะหลักใดๆมารวมกัน เพื่อให้ได้ค่าเท่ากับเลขฐานสิบที่กำหนด จากนั้นเติมเลข “1“ ณ ตำแหน่งที่นำตัวเลขมารวมนั้น เช่น (26)10จะต้องใช้ค่าคงที่เฉพาะรวมกัน 3 หลัก (16+8+2) ดังนั้นจึงเติม “1” ณ ตำแหน่ง
16,8 และ 2 ตามลำดับ ส่วนตำแหน่งที่เหลือให้เติม “0”
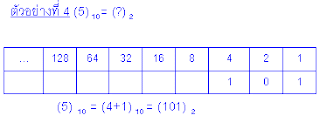

นอกจากนี้ยังสามารถเปลี่ยนค่าจากเลขฐานสิบให้เป็นฐานสอง โดยการหารเลขฐานสิบด้วยสองไปเรื่อยๆจะได้เศษจากการหาร คือ เลขฐานสอง ที่ต้องการ ตำแหน่งของเศษที่เกิดจากการหารก็คือกำลังของเลขฐานสอง นั่นคือเศษที่ได้จากการหารครั้งแรกจะคูณด้วย 20 เศษที่ได้จากการหารด้วย 2 ครั้งที่ 2 จะคูณด้วย 2 1เป็นต้น
ตัวอย่างเช่น

การเปลี่ยนระหว่างเลขฐานอื่น (ระหว่างฐานสอง ฐานแปด ฐานสิบ และฐานสิบหก)
ในที่นี้จะได้อธิบายถึงการเปลี่ยนฐานเลข ระหว่างเลขฐานสอง ฐานแปด ฐานสิบ และฐานสิบหก ซึ่งใช้ในระบบคอมพิวเตอร์ทั่วไป โดยมีหลักการเบื้องต้น 3 ประการ ดังนี้
(a) เปลี่ยนเลขฐานจากโจทย์ ไปสู่เลขฐานสองก่อน (ใช้เลขฐานสองเป็นตัวเชื่อมไปสู่เลข ฐานอื่น)
(b) เลขฐานแปด 1 หลัก ประกอบด้วยเลขฐานสอง 3 หลัก คือ (111) 2
(เนื่องจากเลขฐานแปด ต้องมีค่าไม่เกิน 7)
(c) เลขฐานสิบหก 1 หลัก ประกอบด้วยเลขฐานสอง 4 หลัก คือ (1111) 2
1 1 1 1
(เนื่องจากเลขฐานสิบหก ต้องมีค่าไม่เกิน 15)
ตัวอย่างที่ 7 (75) 8 = (?)10
ตัวอย่างที่ 7 (75) 8 = (?)10
-- ใช้หลักการ (a) เปลี่ยนเลขฐานแปด เป็นเลขฐานสอง ดังนี้

-- แยก (75) 8 ออกเป็น 2 กลุ่มๆละ 3 หลัก ตามหลักการข้อ (b) โดยแยก 7 และ 5 ออกจากกัน ดังนี้

-- เปลี่ยนเลขฐานสองที่ได้ เป็นเลขฐานสิบดังนี้ (111101)2 = (?)10

ตัวอย่างที่ 8 (4C)16 = (?)10
-- แยก (4C) 16 ออกเป็น 2 กลุ่มๆละ 4 หลัก ตามหลักการข้อ (c) ดังนี้
ทำให้ได้จำนวนเลขในรูปของเลขฐานสองเท่ากับ (1001100)2
-- เปลี่ยนเลขฐานสองที่ได้ เป็นเลขฐานสิบดังนี้ (1001100)2 = (?)10
(1001100) 2 = (64+8+4) 10 = (76) 10
\ (4C)16 = (76) 10
การแปลงเลขเศษส่วนในระบบเลขฐานสิบเป็นฐานสอง
การแปลงจำนวนเต็มใช้หลักการหารด้วย 2 (หรือการหาผลบวกของค่าประจำหลักก็ได้) สำหรับการแปลงเศษส่วนใช้วิธีการคูณด้วย 2 (คูณในระบบฐานสิบ) เพื่อหาค่าที่เป็นจำนวนเต็มหรือตัวทด (ตรงกันข้ามกับการแปลงจำนวนเต็มซึ่งใช้การหารและหาเศษที่เหลือ) ค่าตัวทดที่เกิดขึ้นในการคูณแต่ละครั้งให้เก็บไว้เป็นผลลัพธ์ นำส่วนที่เป็นเศษส่วนมาทำการคูณด้วยสองต่อไป จนได้ตัวเลขครบตามจำนวนที่ต้องการ ผู้ศึกษาจงสังเกตด้วยว่าการแปลงเลขเศษส่วนไปสู่ระบบฐานสองบางจำนวนไม่อาจแทนได้อย่างถูกต้อง ปรากฎการณ์นี้เป็นที่มาแห่งความผิดพลาดและคลาดเคลื่อนในการคำนวณเลขในระบบเครื่องคอมพิวเตอร์
ตัวอย่างที่ 9 จงแปลงจำนวน 159.356 ให้เป็นจำนวนในระบบเลขฐานสองกำหนดผลลัพธ์ไม่เกิน 8 หลัก
-- จำนวนที่กำหนดให้มีสองส่วนคือ ส่วนที่เป็นจำนวนเต็มได้แก่
159 แปลงเป็นจำนวนในระบบฐานสองได้ 159 = (10100001)2
-- เศษส่วนคือ .356 ทำการแปลงไปสู่ระบบเลขฐานสองด้วยการคูณด้วย
2 เก็บผลลัพธ์จากตัวแรกไปยังตัวสุดท้าย ดังนี้
ไม่มีความคิดเห็น:
แสดงความคิดเห็น